Home | Manu Jayadharan
Approximations and use of Mathematical Models in Finance, with a focus on Options trading with the help of Greeks.
Author: Manu Jayadharan
Introduction
In this post, I will discuss the pros and cons of financial modeling, specifically in the case of stock option pricing. I will talk about why financial models are imperfect and less predictive compared to models derived from physical laws. I will provide the definition and usage of Greeks from the perspective of a mathematician and share my thoughts on their application.
I have made several simplifications of concepts in this post to make the reading short and comprehensive. I am also talking about modelling of financial instruments and not algorithmic trading which is a different topic.
This post is inspired by a similar post I wrote on Reddit on a related topic. This post can be found here.
What are Options ? Can we model them perfectly ?
- Role of Options: Options are perhaps the most powerul instrument in the trading world, offering the right, but not the obligation, to buy or sell an asset at a predetermined price, making them essential for both trading strategies and hedging risks. The asset or underlying of an option could be anything like stocks, bonds, commodities, etc. It gives the traders an “option” to buy or sell their securities under certain conditions.
Since stock options are the most common type of options (at least from the perspective of mere mortals, aka retail traders like us), I will focus on discussing these options for the remainder of this discussion.
My take on the mathematical interpretation of Greeks in option trading
Introduction
In this post, I will delve into the fascinating world of options and financial derivatives, focusing on the mathematical interpretation of the Greeks and their impact on the pricing of these instruments. Understanding the Greeks is crucial for any trader or investor dealing with options, as they provide insight into the risk and potential profitability of a position.

Understanding the Greeks
Delta (Δ)
Delta represents the rate of change of the option’s price with respect to changes in the underlying asset’s price. It indicates how much the price of an option is expected to move for a $1 change in the price of the underlying asset.
Gamma (Γ)
Gamma measures the rate of change of Delta with respect to changes in the underlying asset’s price. It helps in understanding the stability of Delta and is crucial for assessing the potential risk of large movements in the underlying asset.
Theta (Θ)
Theta represents the rate of change of the option’s price with respect to the passage of time, also known as time decay. It indicates how much the price of an option decreases as it approaches its expiration date.
Vega (ν)
Vega measures the sensitivity of the option’s price to changes in the volatility of the underlying asset. It shows how much the price of an option is expected to move for a 1% change in the implied volatility of the underlying asset.
Rho (ρ)
Rho represents the rate of change of the option’s price with respect to changes in the risk-free interest rate. It indicates how much the price of an option is expected to move for a 1% change in the interest rate.
Pricing of Options
The pricing of options involves various models, with the Black-Scholes model being one of the most widely used. This section will explore how the Greeks play a role in these models and the factors that influence the price of options.
Black-Scholes Model
The Black-Scholes model provides a theoretical estimate of the price of European-style options. It takes into account factors such as the underlying asset’s price, the option’s strike price, time to expiration, volatility, and the risk-free interest rate.
Factors Affecting Option Prices
- Underlying Asset Price: The current price of the underlying asset significantly impacts the price of the option.
- Strike Price: The price at which the option can be exercised affects its value.
- Time to Expiration: The amount of time left until the option expires influences its price, primarily through Theta.
- Volatility: The expected volatility of the underlying asset affects the option’s price through Vega.
- Interest Rates: Changes in risk-free interest rates impact the price of options, as measured by Rho.
Conclusion
Understanding the Greeks is essential for anyone involved in trading or investing in options and financial derivatives. They provide valuable insights into the risks and potential returns of a position. By comprehensively analyzing the Greeks and their impact on option pricing, traders can make more informed decisions and better manage their portfolios.
Thank you for reading! If you have any questions or comments, feel free to leave them below or contact me directly.

My background in a nutshell.
- I am a computational scientist with expertise in numerical analysis, high performance computing, and scientific machine learning. I am interested in application of computational and stastistical learning methods to a wide range of scientific fields including natural sciences, geosciences, physical systems etc. I currently work as a Quantitative Research Analyst for the Citigroup’s Credit Quant group in NYC.
- I have experience in developing and implementing novel algorithms to solve multiphysics CFD problems, using both data-driven deep learning techniques and classical mixed finite element methods (FEM).
- I have many years of teaching experience teaching courses spanning over pure and applied mathematics.
- Currently, I work as a credit quant specializing in pricing and risk management of credit derrivatives in the risk-neutral framework, specifically in LATAM emerging markets.
- I love working on new challenging models and implementing them, while collaborating with others.
- Always looking for new collaborators and interesting projects.
Languages I work with:
- Python for general purpose programming and ML software development.
- C++ for high performance scientific computing and simulations.
Mathematical Skills:
- Numerical Analysis.
- HPC Parallel computing.
- Advanced Probability, Statistics.
- ML,DL.
- Biocomputing.
- Math Finance and Stochastic Calculus.
- Risk Neutral Pricing and Hedging of Credit derrivatives.
- Bonds, CDS, XCCY swaps.
- CFD Computational Fluid Dynamics.
FluidLearn is a software package with python interface, capable of solving non-linear fluid flow problems using supervised deep learning techniques. The solution function and the PDE operator are approximated as neural networks, which will be trained using labelled data.
Conceptually, this API could be used to solve any well-posed PDE system on complex geometric structures, given enough labelled data in the form of boundary and initial conditions. The architecture could also be used for physical parameter estimation and surrogate modelling. As of now, the package is oriented towards PDE systems governing fluid flow problems with many popular flow systems inbuilt. Users have the option to train the model from external data, visualize the training curves, save the model, reload the model, continue training the saved model or make predictions from the saved models.
The package could be seen as an application of the Physics Informed Neural Networks (PINNs) which are artificial neural nets trained with PDE constraints. The idea was first introduced in this publication in 2017. For more details on the mathematical theory behind PINNs, please visit the website maintained by the authors of the aforementioned publication here.
A graphical representation of a feed forward type neural net used in the training is shown below.
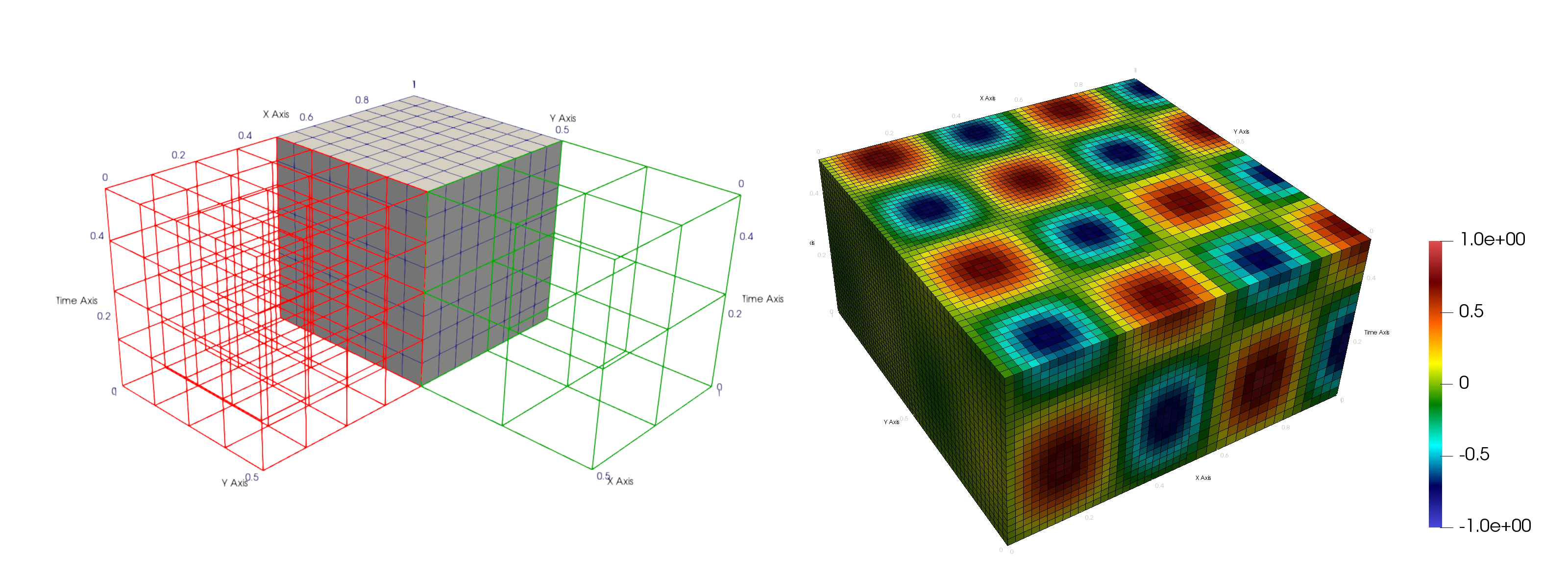
Multiscale Mortar Mixed Finite Element method using novel Space-Time Domain Decomposition (MMMFE-ST-DD)
Fluid flow simulator using multiscale space-time domains.
Full repository can be found here.
Code developed to simulate time-dependent diffusion problem using Multiscale Mortar Mixed Finite Elements(MMMFE). Model can be easily adapted to simulate other fluid flow models based on linear PDEs. The novelty of the simulator lies in using multiple subdomains with variable time steps and mesh size for each subdomain. This give rise to a space-time DD technique allowing non-matching grids for sub-domains in both space and time dimensions. Sub-domain solves are done in parallel across different processors using MPI. Computed solutions are outputted and visualized on a global space-time grid in the .vtk and .vtu formats. Details of the spaces used and rough algorithm can be found in report.pdf and algorithm.pdf respectively. Theoretical results guaranteeing convergence and stability of the problem along with a priori error estimates are proved and being published.
Note:
- The simulator is written using deal.ii FE package which is based on C++.
- All instructions are with respect to a terminal in linux/mac. Please use the ubuntu sub-system if you are using windows 10. A good installation guide for the linux sub-system can be found here.
- Image/animation processing and visualization can be done using paraview. Installation guide can be found here.
Author
Manu Jayadharan, Department of Mathematics at University of Pittsburgh 9/17/2019
email: manu.jayadharan@gmail.com, manu.jayadharan@pitt.edu
researchgate
linkedin